How To Rate A Sports Handicapper
How do you rate a handicapper?
The fact is most handicappers will send out updates only when they have a great run going... but how do you rank a handicapper over the long run?
Before I get to that I want you to look at something.
If you look at the results you will notice that we had one week that wasn't great... in fact Monday to Saturday it was brutal - check it out April 14-19th. I am not ashamed to admit it, we had a bad week... it happens. But the key is bankroll management. After we cashed our two series plays with Montreal Canadiens and Chicago Blackhawks we ended up only losing about 1.7 units on the week... not bad after the way that week started out. The key was bankroll management.
So this brings me to my next point, how do you rate a handicapper?
Who is better?
Handicapper 1 who goes 8-2 (80%) over a week of picks
Handicapper 2 who goes 60-40 (60%) on 100 plays
Handicapper 3 who goes 550-450 (55%) on 1000 plays?
Or the Handicapper who bets underdogs and wins 156.93 units on 129 units wagered across 89 plays? (Like I did in April 2014)
If you are rating a handicapper who often bets underdogs like I do you have to pay attention to units won, units wagered, wager size and number of plays. I will explain further in section 2 below.
Section 1 – Rating handicappers who bet against the spread – Examples 1-3
If you are ranking handicapper who bet against the spread you can use math – specifically the standard deviation and z-score.
If you think about it when you are rating handicappers who pick against the spread you are trying to figure out how rare their results are. Spread bets can be compared to flipping a coin because the results are basically binary (not taking into account pushes)
So what is more unexpected? Flipping a coin and landing on tails 8 out of 10 times or 60 out of 100 or 550 out of 1000?
The first thing we need to figure out is the expected result, I will use 3 examples to illustrate this.
For Handicapper 1 the expected result is 5 out of 10
For Handicapper 2 the expected result is 50 out of 100
For Handicapper 3 the expected result is 500 out of 1000
Next we need to determine the standard deviation how far off the expected result can be explained by random events.
For Handicapper 1 we have 10 events
Standard deviation is probability (in this case 50/50 or .5) * square root of # of plays (in this case 10 plays)
Std = 0.5 * sqrt (10)
= 0.5 * 3.16
= 1.58
Therefore we expect a variance of about 1.58 per 10 events
For Handicapper 2 we can do the same calculation
Std = 0.5 * sqrt (100)
= 0.5 * 10
= 5
Therefore we expect a variance of about 5 per 100 events
For Handicapper 3 we can do the same calculation
Std = 0.5 * sqrt (1000)
= 0.5 * 31.62
= 15.81
For handicapper 3 we expect a variance of 15.81 per 1000 events
So that’s great now what?
Well the next step is to determine the z-score. The z-score is a description of how unlikely an event is with handicappers.
The formula for z-score is observed wins less expected wins divided by the standard deviation
Z = [(observed wins) – (expected wins)] / std
For Handicapper 1
Z = (8-5)/1.58
=1.90
For Handicapper 2
Z =(60-50)/5
=2
For Handicapper 3
Z =(550-500)/15.81
=50/15.81
=3.16
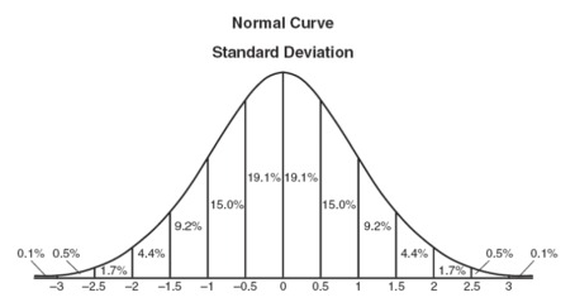
The key metrics to note are the normal distribution.
68% of all handicappers will achieve a z-score of 1 or less
95% of all handicappers will be below a z-score of 2. There for a z-score of 2 puts a handicapper in the to 5% of all handicappers
A z-score of 3 is extremely unlikely. Puts a handicapper in the top 1% of all handicappers see the below image to review the normal distribution with z-score across the bottom.
The fact is most handicappers will send out updates only when they have a great run going... but how do you rank a handicapper over the long run?
Before I get to that I want you to look at something.
If you look at the results you will notice that we had one week that wasn't great... in fact Monday to Saturday it was brutal - check it out April 14-19th. I am not ashamed to admit it, we had a bad week... it happens. But the key is bankroll management. After we cashed our two series plays with Montreal Canadiens and Chicago Blackhawks we ended up only losing about 1.7 units on the week... not bad after the way that week started out. The key was bankroll management.
So this brings me to my next point, how do you rate a handicapper?
Who is better?
Handicapper 1 who goes 8-2 (80%) over a week of picks
Handicapper 2 who goes 60-40 (60%) on 100 plays
Handicapper 3 who goes 550-450 (55%) on 1000 plays?
Or the Handicapper who bets underdogs and wins 156.93 units on 129 units wagered across 89 plays? (Like I did in April 2014)
If you are rating a handicapper who often bets underdogs like I do you have to pay attention to units won, units wagered, wager size and number of plays. I will explain further in section 2 below.
Section 1 – Rating handicappers who bet against the spread – Examples 1-3
If you are ranking handicapper who bet against the spread you can use math – specifically the standard deviation and z-score.
If you think about it when you are rating handicappers who pick against the spread you are trying to figure out how rare their results are. Spread bets can be compared to flipping a coin because the results are basically binary (not taking into account pushes)
So what is more unexpected? Flipping a coin and landing on tails 8 out of 10 times or 60 out of 100 or 550 out of 1000?
The first thing we need to figure out is the expected result, I will use 3 examples to illustrate this.
For Handicapper 1 the expected result is 5 out of 10
For Handicapper 2 the expected result is 50 out of 100
For Handicapper 3 the expected result is 500 out of 1000
Next we need to determine the standard deviation how far off the expected result can be explained by random events.
For Handicapper 1 we have 10 events
Standard deviation is probability (in this case 50/50 or .5) * square root of # of plays (in this case 10 plays)
Std = 0.5 * sqrt (10)
= 0.5 * 3.16
= 1.58
Therefore we expect a variance of about 1.58 per 10 events
For Handicapper 2 we can do the same calculation
Std = 0.5 * sqrt (100)
= 0.5 * 10
= 5
Therefore we expect a variance of about 5 per 100 events
For Handicapper 3 we can do the same calculation
Std = 0.5 * sqrt (1000)
= 0.5 * 31.62
= 15.81
For handicapper 3 we expect a variance of 15.81 per 1000 events
So that’s great now what?
Well the next step is to determine the z-score. The z-score is a description of how unlikely an event is with handicappers.
The formula for z-score is observed wins less expected wins divided by the standard deviation
Z = [(observed wins) – (expected wins)] / std
For Handicapper 1
Z = (8-5)/1.58
=1.90
For Handicapper 2
Z =(60-50)/5
=2
For Handicapper 3
Z =(550-500)/15.81
=50/15.81
=3.16
The key metrics to note are the normal distribution.
68% of all handicappers will achieve a z-score of 1 or less
95% of all handicappers will be below a z-score of 2. There for a z-score of 2 puts a handicapper in the to 5% of all handicappers
A z-score of 3 is extremely unlikely. Puts a handicapper in the top 1% of all handicappers see the below image to review the normal distribution with z-score across the bottom.
As a rule of thumb when selecting a handicapper to follow you should consider both the number of plays they provide in a sample and the number of units wagered and units won - see below for a further description of how to factor in different size unit plays.
Section 2
So how do you rank a handicapper who bets underdog and plus money plays and also varies unit bets?
Well you need to first make sure you are comparing apples to apples.
You must ensure that the units wagered are within a range – following progressive betting strategies are not considered because they are not real handicapping strategies.
A reasonable range is 1-4 units or 1-5 units per play at most.
I am going to use my results from April 2014 to demonstrate how to figure out the z-score for a handicapper who bets underdogs, plus money plays and varies unit strategy.
The first think we should consider is the expected results – now that we are incorporating actual bets with the Juice we need to take that into account.
At -105 lines the average bettor will lose money at approximately 5% per 100 units wagered.
=100/105
=95.2 units returned (a loss of 5% due to the juice)
Betting money lines the spread is often larger as the house lines get further apart. If you are betting a money line at +200 the opposite payout is likely -230 or more.
We will use -110 for this example to be conservative as most of my money line bets don’t exceed a spread of -120.
=100/110
=90.9 units
To turn this into a probability we can take
=1-[1/(expected return)+1]
=1-(52.4%)
=0.476
You average probability of winning works out to .476 (we will use this in place of the .5 in the mean and z-score calculation)
We will use the number of bets placed to calculate the expected variance
Std = 0.476 * sqrt (89)
= 0.476 * 9.43
= 4.49
On 89 units wagered we would expect a standard deviation or variance of 4.49
BUT we also have to take into account the average bet size and the odds, before we compare this number to the results observed.
If you look at my aggregate bets I risked a total of 129 units to win a potential of 168.68 units
My average unit size per bet was:
= 129/89
=1.449
This increases the Standard deviation to
=4.49 * 1.449
=6.50
Average bet is
=168.68/129
=1.308
Or American odds of about +131
This increases the Standard deviation to
=6.5*1.31
=8.51
Recall from above
Z = [(observed wins) – (expected wins)] / std
In this case
Z = [(observed return) – (expected return)] / std
Since I bet 129 units we can calculate the expected return of
=129/110
=117.27
My observed return was the actual amount that we won which was 156.93 units
=156.93
Z = (156.93-117.27)/8.51
= 39.66/8.51
= 4.66
*Things to note –
My April results had the Masters tournament included where we won 7 units on 10 wagered. If we remove the Masters tournament the results actually increase to a z-score of 5.45
These calculations are compared to the average population. You may want to factor in a winning % of 5% to compare these results against top handicappers.
The average winning handicapper wins just a small % above 52.4% of their bets to cover the juice. A very good handicapper can return about 5% on their money wagered.
If you increase the expected wins to 5% that would chance the z-score as follows
Expected wins = 129*1.05
=135.45
Z =(156.93-135.45)/8/51
=21.48/8.51
=2.52
The Z-Score drops considerably but still rates in the top 0.5% of the population of winning professional handicappers.
This money we returned 21.7% on our money wagered these results are in the top 10th of the top 10th of 1% of the population. If you stick to a basic unit strategy and follow the wagers as posted you will become rich very very quickly with results like this… note these results 100% real and were sent to clients – however past results do not necessarily reflect future performance.
To conclude
Most handicappers are scared of this number because it highlights how average or actually bad they really are. Winning handicappers are rare, and most handicappers make it virtually impossible to calculate this as they don’t provide complete results or only show win%.
Other factors to consider:
Slippage – you can expect a slippage of approximately 5-10% when following a good handicappers bets. This is impossible to avoid. This is due to the sports books rebalancing their lines. If a good handicapper notices a line, approximately 5-10% of the time the line will have moved by the time you receive the email or text message. This can be frustrating but is generally the sign of a good handicapper.
If a handicapper is consistently sending out stale lines you should be careful. Shading lines is the oldest trick in the book for scamdicappers. One way to check this is to look at the time you receive the email and compare the line posted to the lines by time on a service like sports insights. Sports Insights shows you the times when the lines in Vegas move. This is generally a pretty reliable measuring stick.
Section 2
So how do you rank a handicapper who bets underdog and plus money plays and also varies unit bets?
Well you need to first make sure you are comparing apples to apples.
You must ensure that the units wagered are within a range – following progressive betting strategies are not considered because they are not real handicapping strategies.
A reasonable range is 1-4 units or 1-5 units per play at most.
I am going to use my results from April 2014 to demonstrate how to figure out the z-score for a handicapper who bets underdogs, plus money plays and varies unit strategy.
The first think we should consider is the expected results – now that we are incorporating actual bets with the Juice we need to take that into account.
At -105 lines the average bettor will lose money at approximately 5% per 100 units wagered.
=100/105
=95.2 units returned (a loss of 5% due to the juice)
Betting money lines the spread is often larger as the house lines get further apart. If you are betting a money line at +200 the opposite payout is likely -230 or more.
We will use -110 for this example to be conservative as most of my money line bets don’t exceed a spread of -120.
=100/110
=90.9 units
To turn this into a probability we can take
=1-[1/(expected return)+1]
=1-(52.4%)
=0.476
You average probability of winning works out to .476 (we will use this in place of the .5 in the mean and z-score calculation)
We will use the number of bets placed to calculate the expected variance
Std = 0.476 * sqrt (89)
= 0.476 * 9.43
= 4.49
On 89 units wagered we would expect a standard deviation or variance of 4.49
BUT we also have to take into account the average bet size and the odds, before we compare this number to the results observed.
If you look at my aggregate bets I risked a total of 129 units to win a potential of 168.68 units
My average unit size per bet was:
= 129/89
=1.449
This increases the Standard deviation to
=4.49 * 1.449
=6.50
Average bet is
=168.68/129
=1.308
Or American odds of about +131
This increases the Standard deviation to
=6.5*1.31
=8.51
Recall from above
Z = [(observed wins) – (expected wins)] / std
In this case
Z = [(observed return) – (expected return)] / std
Since I bet 129 units we can calculate the expected return of
=129/110
=117.27
My observed return was the actual amount that we won which was 156.93 units
=156.93
Z = (156.93-117.27)/8.51
= 39.66/8.51
= 4.66
*Things to note –
My April results had the Masters tournament included where we won 7 units on 10 wagered. If we remove the Masters tournament the results actually increase to a z-score of 5.45
These calculations are compared to the average population. You may want to factor in a winning % of 5% to compare these results against top handicappers.
The average winning handicapper wins just a small % above 52.4% of their bets to cover the juice. A very good handicapper can return about 5% on their money wagered.
If you increase the expected wins to 5% that would chance the z-score as follows
Expected wins = 129*1.05
=135.45
Z =(156.93-135.45)/8/51
=21.48/8.51
=2.52
The Z-Score drops considerably but still rates in the top 0.5% of the population of winning professional handicappers.
This money we returned 21.7% on our money wagered these results are in the top 10th of the top 10th of 1% of the population. If you stick to a basic unit strategy and follow the wagers as posted you will become rich very very quickly with results like this… note these results 100% real and were sent to clients – however past results do not necessarily reflect future performance.
To conclude
Most handicappers are scared of this number because it highlights how average or actually bad they really are. Winning handicappers are rare, and most handicappers make it virtually impossible to calculate this as they don’t provide complete results or only show win%.
Other factors to consider:
Slippage – you can expect a slippage of approximately 5-10% when following a good handicappers bets. This is impossible to avoid. This is due to the sports books rebalancing their lines. If a good handicapper notices a line, approximately 5-10% of the time the line will have moved by the time you receive the email or text message. This can be frustrating but is generally the sign of a good handicapper.
If a handicapper is consistently sending out stale lines you should be careful. Shading lines is the oldest trick in the book for scamdicappers. One way to check this is to look at the time you receive the email and compare the line posted to the lines by time on a service like sports insights. Sports Insights shows you the times when the lines in Vegas move. This is generally a pretty reliable measuring stick.